Este tipo de medidas nos permiten identificar y ubicar el punto (valor) alrededor del cual se tienden ha reunir los datos (“Punto central”). Estas medidas aplicadas a las características de las unidades de una muestra se les denomina estimadores o esta-dígrafos; mientras que aplicadas a poblaciones se les denomina parámetros o valores estadísticos de la población. Los principales métodos utilizados para ubicar el punto central son la media, la mediana y la moda.
MEDIA:
La media es la medida mas usada para encontrar el promedio. De hecho, la gente siempre utiliza la palabra " promedio " para referirse a la " media ".Encontrarla es simple: solo suma todos los números en los datos y divídelos por la cantidad de los números .

FORMULA PARA HALLAR LA MEDIA
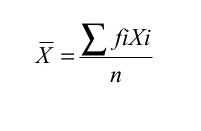

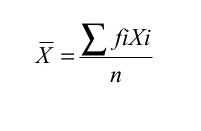
= 6800 =136
50
136 libras peso promedio de los alumnos
MEDIANA: La mediana es el numero del medio en un grupo de datos. Sin embargo, los datos deben estar ordenados numéricamente ( de mayor a menor o de menor a mayor ) antes de encontrar este promedio. Si el numero del medio esta entre dos números, entonces encuentra la media entre esos dos ( sumalos y divídelos entre 2) mediana: el numero del medio en un grupo de datos.
FORMULA PARA HALLAR LA MEDIANA
MODA:
La moda es probablemente la forma menos común de encontrar el promedio, y en la mayoría de los casos es la menos útil. Para encontrar la moda, solo encuentra el numero que mas se repite. Puede haber mas de una moda, o ninguna.
moda: numero que mas se repite
FORMULA PARA HALLAR LA MODA
Los cuartiles son valores que dividen una muestra de datos en cuatro partes iguales. Utilizando cuartiles puede evaluar rápidamente la dispersión y la tendencia central de un conjunto de datos, que son los pasos iniciales importantes para comprender sus datos.
| Primer cuartil (Q1) | 25% de los datos es menor que o igual a este valor. |
| Seg. cuartil (Q2) | La mediana. 50% de los datos es menor que o igual a este valor. |
| Tercer cuartil (Q3) | 75% de los datos es menor que o igual a este valor. |
significa que el 11% de los alumnos tienen un peso de hasta 123.75 Lb
signigica que el 20% de los estudiantes tienen un peso menor o igual a 134.61 libras
significa que 31% de los estudiantes tienen un peso menor o igual a 144.51 libras





No hay comentarios:
Publicar un comentario